Effective Interest Rate Calculator
Easy-to-use effective interest rate calculator shows your real rate of return or interest
rate when
accounting for compounding. Know
what you are paying or making before choosing an investment or
loan.
Effective Interest Rate Calculator Reveals Your Real
Interest
Rate or Rate of
Return
When making investments or paying back loans, it’s important to understand how compounded interest affects your returns or payment amounts over the years. Our Effective Interest Rate Calculator saves you the hassle of calculating and shows you the effects of compounding on interest.
When you are making or paying interest that involves compounding, there is the stated interest rate (also called the nominal interest rate), and then there’s the effective interest rate. The stated rate doesn’t take into account compounding, while the effective rate does.
Consider a simple example of getting paid 10% per year for two years. You invest $1,000, and at the end of one year you have $1,100 ($100 gain). If you keep that whole amount in the investment until next year, you still make 10% – but you now have a larger amount of capital, so at the end of two years you have $1,210 ($110 gain). This means you will have made an extra $10 in the second year compared to the first.
You did make 10% each year based on your starting balance. That is the stated interest rate. But your total gain over the period is 21% ((1210 - 1000) / 1000); that’s your effective rate over the entire two years. The effective rate per period (each year) is 10%.
In this case, because you are benefiting from compounding, your effective rate of return is higher than the stated rate of return.
This can also work against you. If you are paying 5% interest but it compounds monthly, your interest rate is actually higher than 5%.
Effective Interest Rate Calculator Input Fields
Here’s how our effective interest rate calculator works, as well as what each of the input fields means.
All three input fields are required in order to get the effective rate. If you don’t know all the information to input, you can try out different numbers, or provide an estimate, to see the effect on the answers.
Nominal Rate
This is the stated interest rate, usually quoted as a yearly number (but it could be some other time frame, such as monthly or daily). This can be a return percentage or an interest percentage
Compounding Per Period
This is how many times the interest or return compounds within one period.
If the nominal rate is quoted in years, then input how often the interest/return compounds within one year. If the nominal rate you used is for one month, then input the compounding frequency for one month.
Number of Periods
This is how many periods you will be paying interest or receiving the Nominal return. Keep the periods the same as the Nominal Rate. For example, if the Nominal Rate is quoted yearly, then your Number of Periods is in years.
If the Nominal Rate is quoted monthly, then the Number of Periods is how many months you will be paying interest or receiving a return.
What the Effective Interest Rate Calculator Answers Mean
The numbers you put into the input fields will affect the answers the calculator produces. Here’s what each of the output or answer fields means.
Effective Rate Per Period
This is the actual rate of return you receive, or actual interest you‘re paying when accounting for compounding.
The greater the frequency of the compounding per period, the higher the Effective Rate Per Period compared to the Nominal Rate.
If the interest (or return) only compounds once per period, then the Effective Rate Per Period and the Nominal Rate will be the same.
Effective Rate for Total Number of Periods
This is the total return or total amount of interest that is paid over the entire number of periods.
This calculation takes into account the total number of periods, whereas the other two calculations are per period. Even if interest only compounds once per period (which results in the same answer as the Nominal Rate), the Effective Rate for the Total Number of Periods includes the compounding over all periods, and will thus be higher than simply multiplying the Nominal Rate x Number of Periods.
Rate Per Compounding Interval
This shows the rate of return or interest rate for fractions of a period. If Compound Per Period is 1, then the Rate Per Compounding Interval will be the same as the Nominal Rate.
If the Compounding Per Period is set to 2, then the Rate Per Compounding Interval is showing the rate for every 6 months (assuming a period is one year).
If the Compounding Per Period is set to 12, then the Rate Per Compounding Interval is showing the rate per one month (1/12 of a year), assuming a period is one year.
Effective Interest Rate Example
Here’s a real-world example of how you can use the Effective Interest Rate calculator, assuming you have the data to input the nominal rate, the compounding frequency, and the number of periods.
You don’t need to know all these variables; you can estimate them, or input different numbers to see how the outputs change.
Remember that effective rates can apply to both interest payments and investment returns.
Assume that your bank is offering a 5% (yearly stated rate) Certificate of Deposit, where interest is compounding daily. In order to receive the interest, you can’t pull the funds out for one year. You could also keep it in for two, three or more years if you wish. The calculator shows your effective rate on this investment – which will be higher than 5%, because there is compounding.
You would plug 5% into the Nominal Rate field, 365 into the Compounding Per Period Field, and 1 into the Number of Periods.
Recall that you will need to keep your periods steady based on the stated rate. In this case, an annual rate was provided, and compounding occurs daily. There are 365 days in a year. The investment must be held for one year, so that is the Number of Periods.
The Effective Rate Per Period is the effective rate for the entire year. Since your money is being compounded daily, you are actually making 5.13% for the year, which is more than the stated 5%.
Since this example only looks at one period, the Effective Rate for the Total Number of Periods is the same as the Effective Rate Per Period. If there were more periods, the Total Number of Periods return/interest would be higher.
The Rate Per Compounding Interval is daily, in this case, since our compounding interval is daily (365 days in a year).
If you hold this investment for two years, everything stays the same, except you put 2 into the Number of Periods. The Effective Rate for Total Number of Periods increases to 10.52% to reflect your total return, including compounding, over the entire two-year period.
Frequently asked questions
1. What is the effective interest rate formula?
This is the formula for calculating effective interest, where r is the effective interest rate, i is the stated interest rate, and n is the number of compounding periods.
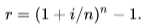
2. What is the difference between an effective interest rate and an interest rate?
The interest rate, often called the “nominal” or “stated” rate, doesn’t take into account the effect of compounding. The effective rate may therefore be higher than the stated interest rate if there is compounding.
3. How can I calculate effective interest on a loan?
You will need to know the stated interest rate, the compounding frequency, and the number of periods you will be repaying the loan. Interest is often calculated/compounded daily, like on credit cards, but interest rates are often quoted in years. Therefore, in an effective interest rate calculator, input your yearly interest rate, 365 as the compounding period, and 1 year as the number of periods to estimate your effective interest rate on a loan per year.
4. How can I calculate effective interest on an investment?
You will need to know the estimated or stated rate of return on the investment, as well as how often the return compounds and how many years you plan to hold the investment. Since investments are often quoted as yearly percentages, the return may only compound once per year. Plug the stated rate of return, one compounding per period, and how many years you plan to hold the investment into an effective interest rate calculator to see your effective rate of return.
6. What’s the difference between simple interest and compound interest??
Simple interest calculates interest on the original balance. It does not take into account the effect of compounding, or paying interest (or receiving a return) on a growing balance as interest is accumulated on the original balance. Compound interest is when you make interest on the original balance plus the interest received.
7. What are common compounding periods?
Daily compounding is common. Monthly compounding and yearly compounding are also used frequently. Continuous compounding is when interest is compounding continuously at the smallest increment of time. You may also see quarterly compounding or semi-annual compounding.
Final Thoughts on Using an Effective
Interest Rate
Calculator
The stated or nominal rate of interest or return isn’t always the same as the effective rate of return. The effective rate of return/interest takes into account compounding, while the nominal rate doesn’t.
Using an effective interest rate calculator is relatively simple, assuming you maintain a consistent period of time throughout. If a rate is provided as a monthly figure, then your Number of Periods should be in months, and Compounding per Period is how many times it compounds per month. If it is an annual interest rate, then the Number of Periods is in years, and the Compounding per Period is how many times it compounds per year.